[二项数据和二元数据的关系]属性数据分析｜第三章-广义线性模型-01~03-GLM的成分、二元变量的GLM、计数变量的GLM

以后他们的着眼点在 two-way 列联表的预测上，不过现实生活中的统计数据可能闻所未闻两个说明表达式，所以这些说明表达式有可能是已连续的，有可能是特性统计数据，只好 two-way 列联表就不如用了。

从第一章开始，他们的着眼点迁移到了对特性积极响应表达式的数学模型构筑上。

第一章，他们将笼统地如是说狭义非线性数学模型：狭义非线性数学模型的四个重要组成部分[第一节]、相互依赖表达式（binary responses）的狭义非线性数学模型[第一节]、算数表达式 (counts) 的狭义非线性数学模型和成分股族的均方表达式[第二节]、GLM的推测与数学模型确诊[第二节]、怎样解均方表达式进而获得模块的计算结果[第六节]。

除此之外，方法论重回数学模型 (logistic regression model) 的技术细节将在第4章至第6章展开具体内容的如是说，成分股函数非线性数学模型 (loglinear model) 的技术细节则在第7章展开具体内容如是说。

自述他们以后学的非线性重回，有关模块和差值的各式各样推测都是创建在环域假定上的。狭义非线性数学模型与一般的非线性数学模型较之主要有两个不同：

积极响应表达式的原产可以非环域【非线性重回他们假定国际标准差环域，所以未知 ， 也环域】可视化并不是间接对 展开，而要对 展开。

为的是更快地饮用狭义非线性数学模型，他们先要查阅它的外包装：

狭义非线性数学模型的基本上形成就在下边这张外包装中了。

为的是使先期的自学更为简洁，他们这儿填入两个Chavanges——怎样将一些常用的原产写出概率原产族的国际标准方式？

只好他们可以看出：

对顶角原产的典型联系为 logit 表达式 ，由此获得的狭义非线性数学模型（对顶角原产+logit link）他们称为 logit model。对相互依赖(binary)统计数据，他们通常使用这个数学模型。泊松原产的典型联系为 log 表达式 ，由此获得的狭义非线性数学模型（泊松原产+log link）他们称为 Poisson loglinear model。对算数表达式（counts）他们会使用这个数学模型，当然当均值与国际标准差明显不相等的时候，也会用负对顶角原产作为积极响应表达式的原产，因为负对顶角原产的国际标准差比均值会多出一项。国际标准差未知的环域原产的典型联系为 ，他们把这个联系称为 identity link。对满足环域原产的已连续表达式，他们可以对 使用 odinary regression 数学模型（环域原产+identity link）。当然，link function 也可以不选择典型联系。选择典型联系的好处是因为在估计模块的时候他们可以获得较为漂亮的方式。

相互依赖表达式其实他们已经很常用了——成功 or 失败，是 or 否...，这些问题都可以转化为试验的成功与否。他们记积极响应表达式为 ， 满足 , .他们假定每两个观测 都是两个伯努利随机表达式。

这儿为的是简化，他们仅考虑两个说明表达式。由于 的值可以随着 的变化而变化，他们记为 。

这儿他们如是说的不同的数学模型，主要区别就是在于link function 的不同。对相互依赖积极响应表达式，常用的有identity link、logit link、inverse CDF link。

非线性概率数学模型 （Linear Probability Model）

， ， [这儿使用的是 identity link]

非线性概率数学模型： 。存在的问题：由于 的取值是整个实轴，故当 非常大或者非常小的时候，数学模型获得的 将超过 ，这就不能用来说明概率了。因此这个数学模型只适合 的取值范围非常有限的情形。拥有的好处：当数学模型可行的时候，它易于说明—— 代表了 变化两个单位时 的变化量。若积极响应表达式服从的是环域原产，模块的ML估计与最小二乘估计是一样的，不过他们假定的为对顶角原产啊——这时候他们使用的方法为ML估计。具体内容怎么估留在后边的section讲。

方法论重回数学模型 (Logistic Regression Model)

为的是解决预测落在 之外的问题，他们考虑 与 之间的非非线性亲密关系。在现实生活生活中， 通常是单调的，呈现出S曲线。为的是刻画这样的特征，他们使用logit link。

方法论重回数学模型： 的大小决定了曲线增长的快慢。当 时，随 增加， 增加；当 时，随 减少， 减少。

Probit 数学模型 (Probit Model)

他们知道对已连续随机表达式来说，CDF表达式的值域一定在 之间，所以也会有近似S曲线的效果。这启示他们去用两个CDF 去等于 。

他们用 来表示国际标准环域原产的CDF。所以他们可以写出

Probit 数学模型： ; 这儿 允许曲线左右移动， 决定曲线的增长速率。当 的反表达式存在时，他们有 。这时他们的link function就是 。

对算数表达式而言，最出名的数学模型莫过于将积极响应表达式 的原产假定成为泊松原产。事实上泊松原产是由对顶角原产近似来的。泊松原产发明的初衷是为的是描述 次试验中，若一次试验成功的概率为 ，所以试验成功的均值为 。下边为的是保持记号的一致性，他们用 来代替 表示均值。

泊松成分股函数非线性数学模型 (Poisson Loglinear Models)

。对假定为服从泊松原产的积极响应表达式，常用的link 为 log link。

，所以 增加两个单位， 将扩大 倍。

书上给出的是母鲎及其追随者的例子。对每只母鲎，研究者们统计了它的颜色(color)、棘刺状况(spine)、甲壳宽度(width, cm)、重量(weight,kg)、和栖息在这只母鲎附近的公鲎的数量(satellites )。这儿，积极响应表达式为追随者(公鲎)的数量，其它的都是可能的说明表达式。

研究者们先选取了两个说明表达式：甲壳宽度。若间接观察个体的统计数据，甲壳宽度与追随者个数的亲密关系趋势并不明显。

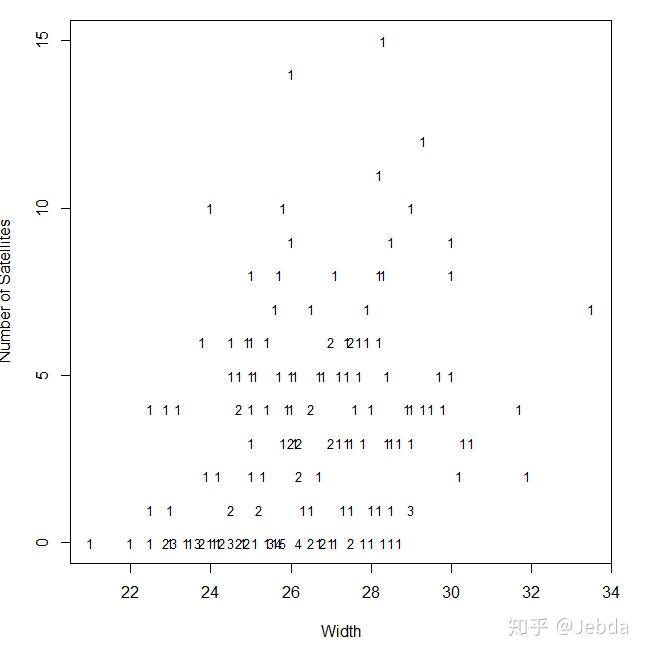
只好研究者将母鲎按照宽度展开了分组，并计算了每个组中母鲎追随者的样本平均数与样本国际标准差。分组之后甲壳宽度与追随者个数的正相关趋势变得明显了。

接着，研究者们用原始的统计数据拟合了成分股函数非线性数学模型

获得的宽度前边的系数为0.164。

当然他们也可以使用identity link:

获得宽度前边的系数为0.55。这暗示着宽度增加大约2cm就会多两个追随者。

注意到泊松原产的均值与国际标准差是相同的，不过他们分组计算均值与国际标准差发现，事实似乎并不是这样，统计数据出现了超散布性（overdispersion）。

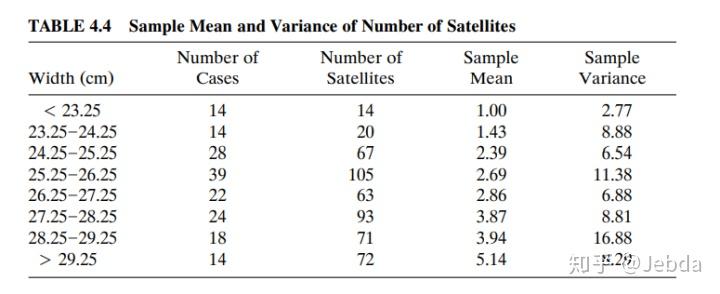
为的是解决这个问题，他们可以用负对顶角原产来展开拟合——因为这个原产的国际标准差含有两个散布模块。

比率的泊松重回

当事件在特定的时间、空间...下发生，他们可能会事件发生的比率更感兴趣。当算数积极响应表达式具有指标 ，所以有关这个指标的样本比率为 。当 时，比率的期望是 。他们可以把数学模型写为： 。

上述的讨论他们发现只有环域假定+identity link的情形他们可以获得与OLS估计一样的显式解，其它的情形他们无法获得具体内容的表达式，需要通过计算方法来获得他们需要的模块。但有一点可以肯定的是，典型联系的应用大大简化了他们的解，如果他们采用的是非典型联系，求导的过程中 就没这么可爱了。用算法具体内容怎样解，他们就等到下次课再来看吧~